Binary Search

Binary Search is a O(log n) algorithm for finding a specific element x in a sorted array of elements. The algorithm repeatedly eliminates half of the array based on a comparison with the middle element.

The problem

Given a sorted array of n elements (integers, strings, etc.) and a search element x. Return the index of x in the array, or -1 if x is not in the array.

In practice we often need to determine if a given element is contained in an array. Consider for example a phone company that sells phone numbers to its customers. The company has an array of all available phone numbers. They can only sell a given number if it is contained in the array. Binary Search is an efficient algorithm to use in such situations.

Examples

Note: If you have never seen the algorithm before, check the Algorithm Description section first.

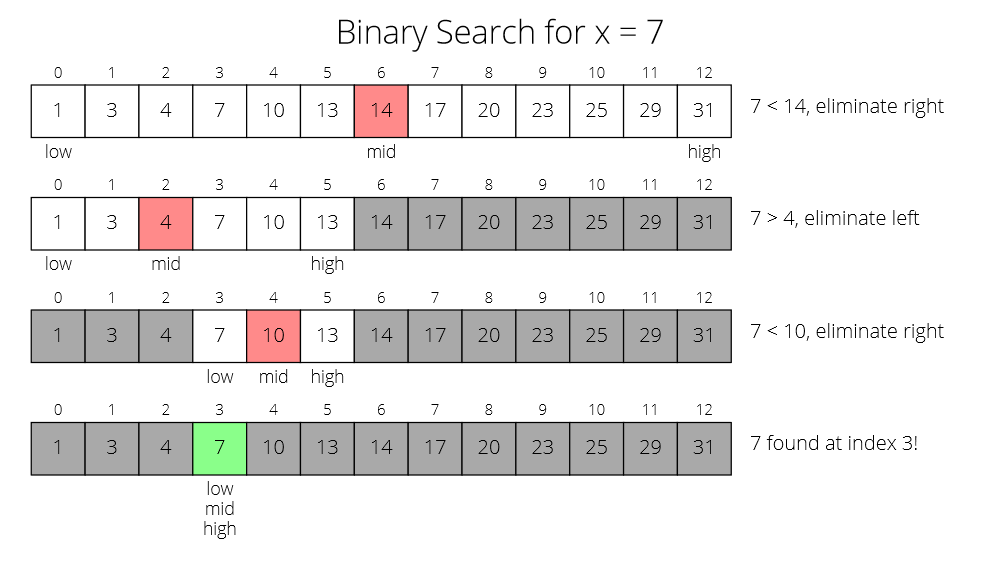
In the first example we successfully find the element we are searching for:

In the next example we search for an element not contained in the array:

Algorithm Description

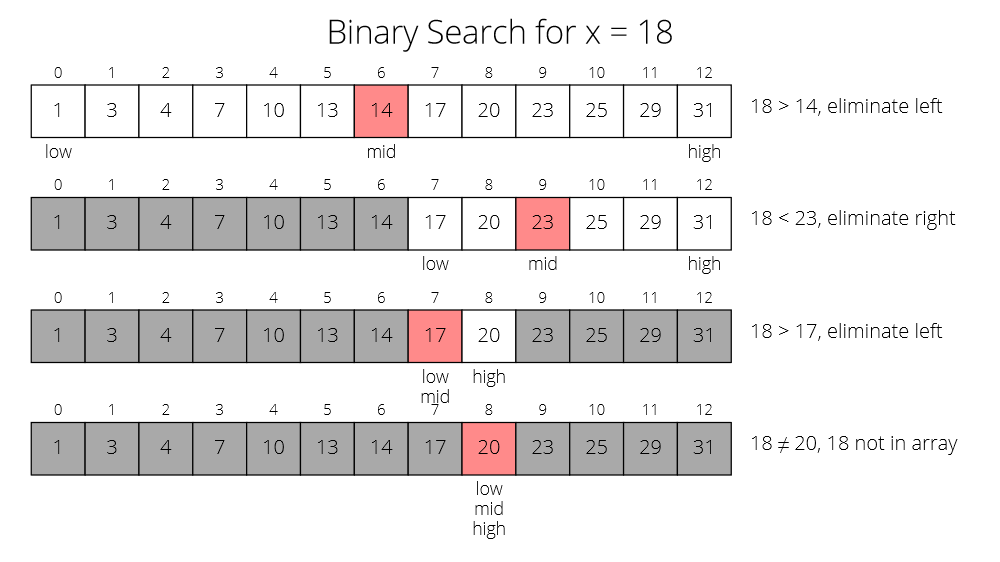
Important: The array that we are searching through must be in sorted order for the algorithm to work.

• Set low = 0 and high = n-1 (these are limits of the search interval)
• Repeat the following until x is found, or the search interval is empty:
• • Compare x to the middle element, with index mid = ⌊(low + high) / 2⌋
  • If x = array[mid]: return mid (x was found at that index)
  • If x > array[mid]: set low = mid+1 (x is also greater than every element left of mid)
  • If x < array[mid]: set high = mid-1 (x is also smaller than every element right of mid)
• Return -1 (x is not in the array)

Running Time

At each step of Binary Search, we can eliminate at least half of the search interval. In the worst case, we will eliminate exactly half of the search interval pr. step. We can halve the interval log₂(n) times before just one element remains. In the end, we also have to check if the remaining element is the search element. This gives us a maximum of log₂(n) + 1 comparisons, which makes Binary Search an O(log n) algorithm.

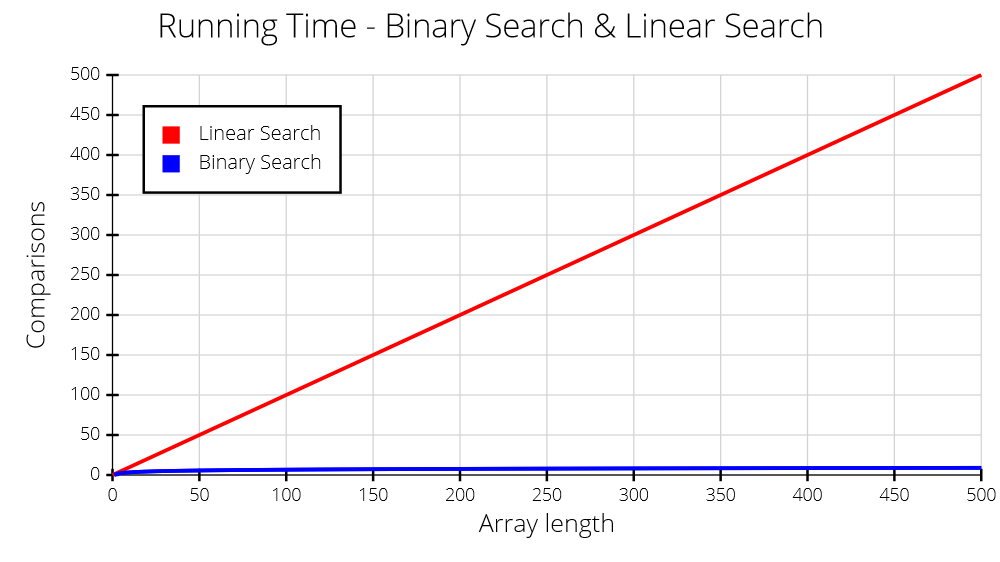
The table below shows the maximum number of comparisons needed for Binary Search and Linear Search (checking every element one by one).

Max. Comparisons

Array Length	Linear Search	Binary Search
10	10	4
102	102	7
103	103	10
104	104	14
105	105	17
106	106	20
107	107	24
108	108	27
109	109	30

The plot below shows the difference in running time visually. Note how the gap between Binary Search and Linear Search increases with the size of the array.